Find the maximum positive and negative shear force:

Find the maximum positive and negative shear force at point P in beam of Figure which is crossed by two connected wheel loads 3 m aparts moving from right to left. The front wheel carries a load of 20 kN and the rear wheel 10 kN.

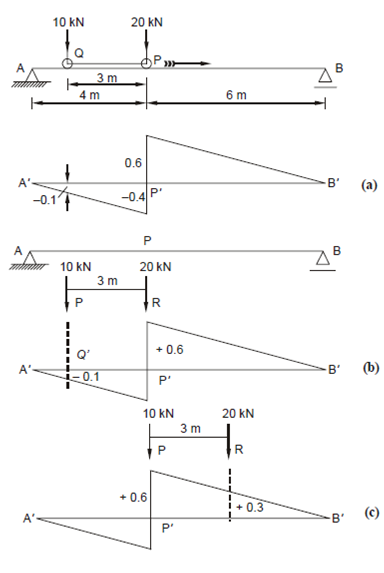
Solution

Maximum Negative SF

For maximum negative shear force at P, the heavier wheel (20 kN) should be placed just to the left of P, the other wheel (10 kN) will then lie at Q which is 3 m to left of P (Figure 8(a)). The ordinate of IL diagram at P is - 0.4 and in which at Q is - 0.1 (by same triangles).

Hence, maximum negative shear force at P,

V_P = 20 × (- 0.4) + 10 (- 0.1) = - 9 kN.

Maximum Positive SF

Here, two cases need to be examined

(a) When the heavier wheel 20 kN is just crossed to right of P, and the lighter wheel (10 kN) is at Q 3 m behind it (Figure 8(b)). Hence the shear force

V_P = 20 × (+ 0.6) + 10 × (- 0.1) = 11 kN.

(b) When the lighter wheel (10 kN) has just crossed to right of P and the front wheel (20 kN) is 3 m to right of it at R as in Figure 8 (c).

The ordinate of IL diagram at P is + 0.6 and at R it is + 0.3.

Hence, shear force V_P = 20 × (+ 0.3) + 10 × (+ 0.6) = 12 kN.

The second position gives the higher value; hence, the maximum positive SF will be 12 kN.