Definition:  Given  the  discount factor  6,  the present value  of  the  infinite sequence of payoffs n₁,  n₂, n₃,. is given by

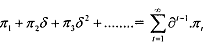
Let us consider the infinitely repeated prisoners' dilemma, where the payoff of the players  is the  present  value of the player's  payoff from the stage games. The discount factor  is  d  for  both  the players.  We  want to show that cooperation, that  is, (Ml, M2) can occur  in  every stage of a sub-game-perfect outcome  of  an  infinitely repeated game, even though  the  only  Nash
equilibrium in the stage game is cooperation, which  is (L1, L2).

Suppose the  i"  player begins the infinitely repeated game by  cooperation and then  cooperates  in  rest  of the periods  if  and  only  if  both the players  have cooperated  in  the previous stages of the game. Formally, the strategy of the ith player is Play Mi in the first stage In  the  tth  stage  if  the outcome  of all  the  preceding  (t-1)  has  been  (MI, M2) then play Mi in the th  stage otherwise play Li, (i = 1, 2) (This type of strategy is  called  a  trigger strategy). If both  the player follows  this  trigger strategy,
then the outcome of the infinitely repeated game would be (MI, M2)  in every stage of the game. Now we will prove that given some conditions on the value of d, the above trigger strategy is a Nash equilibrium of the  infinitely repeated game, and such an equilibrium is sub-game-perfect.

To show that the above described trigger strategy  is a Nash equilibrium of  the game, we have to show that  if  the player i  adopts the trigger strategy, the best response of the player j  is to adopt the same strategy. The present value of the payoffs that will  be  generated, for the jth  player,  if both of the players stick to the trigger strategy is given by  

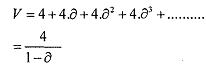
If  the jth  player deviates from  the  trigger strategy, that is, she plays LJ  in  the first stage, which will  eventually lead to non-cooperation from player  i  in  the second  stage  (Li)  and  consequently  from  player  j  (Lj)  also,  the discounted payoff of  the jth  player  is  given  by  (the  payoff  of  the  first stage  for  the jh player would  be  5,  as  the  ith  player  in  the  first period following  her  trigger strategy will play Ri, and for the remaining periods the payoff of the  jth  player would be  1)

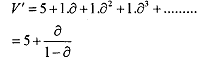
Therefore, playing Mj, or  following the  trigger strategy is optimal for the jth player given that the  ith player sticks to her trigger strategy if and only if

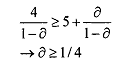
Therefore, the trigger  strategy  is  the Nash  equilibrium  for both  the players if and only  if δ>1/4.

Now we are  in  a  position  to  formally  define  an  infinitely  repeated  game, history, strategy and sub games of an infinitely repeated game.