Definition of Infinitely Repeated Game:

Given a stage game G,  let G (m, d) denote the  infinitely repeated game in which G  is repeated forever and  all the players have  the  same discounting  factor  denoted by  a.  For each t  (t is  a positive  integer),  the outcomes of the t-l  previous plays  are observed before the tth  stage begins. Each player's payoff  in G (m, d) is the present  value of the player's,payoff from the infinite sequence ofthe  stage game.

History of an Infinitely Repeated Game: In the finitely repeated game G(T) or the  infinitely  repeated game G  (m, d), the history  of play through stage t  is the record of the player's  choices in  the stage 1  through t. Strategy  of  an Infinitely Repeated  Game:  Notice while defining the repeated  game in  section we used the notation 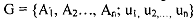while  in  previous units we described a static game of complete  information as 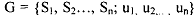remember  Si is  in  a static game of complete informatim  implies strategy spaces whereas the Ai s  in  a dynamic or repeated game  of  complete  information implies  the  action  space.  The players might have chosen  (al  ,, a21,  as,,.  . . anl)  in  stage  1  (suppose there are n players)  and 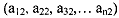and so on. For each player  i  and for each stage s, the action a,, belongs to the Action space Ai. Thus,  in  an infinitely repeated game there  is a difference between strategy and actions. In a finitely repeated  game G(T) or an  infinitely repeated game G (m, a), a player's strategy specifies the action the player will  take  in every stage of the  game,  for  each possible  history  throughout the  game.  So, strategy  is  a complete  plan  of action. It  is defined  for each possible circumstance and  for every stage of an infinitely repeated game.