Series Opposing:

Figure illustrates two coils coupled in series opposition as their fluxes are in opposite direction as per dot convention.

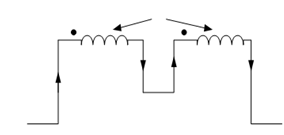
 Figure: Inductive Coupling in Series (Flux Opposing)

Let us consider coil 1 and coil 2 individually.

Coil 1

Self-induced e.m.f e  =- L₁  (di /dt)

Mutually induced e.m.f e₁′ = M (di /dt)  [due to change of current in coil 2]

Coil 2

Self-induced e.m.f e₂  =- L₂  (di /dt)

Mutually induced e.m.f e₂′ = M(di/dt) [due to change of current in coil 1]

Therefore the total induced e.m.f of the combination can be written as

e = e₁  + e₂  + e₁′ + e₂′

e =- L₁  (di /dt) - L₂( di/ dt) + 2 M (di/dt) =- (L₁ + L₂  - 2M ) (di/dt)

If L is the equivalent inductance of the combination, then we may write

e =- L( di/ dt)

From Eqs (39) and (40), we get

- L (di / dt )= - (L₁  + L ₂ - 2M ) (di /dt)                                 

or, L = L₁  + L₂  - 2M