Torque-Slip (T-S) Characteristics:

For the better expression of the torque make thevenin's equivalent circuit for the left side of the terminal 1-2.

The thevenin impedance.

Z¯T  = (R₁ + j X₁ ) | | j X _m  = R_T  + j X_T

Thevenin voltage

V¯_T  = V₁ ( j X _m / ( R₁ + j X₁ + j X _m ))

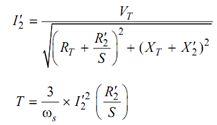
Substitute the value of I₂′ in Eq.

T =  3/ ω_s  .  (V _T) ² (R₂′ /S) /(R_T +( R₂′/S)² +(X_T + X₂ ′)²

Eq. (57) expresses the torque as a function of voltage and slip. This is seen that for a fixed value of slip, torque is equal to proportional to the square of voltage. Figure illustrates the torque slip characteristics of an induction motor for the rated voltage.

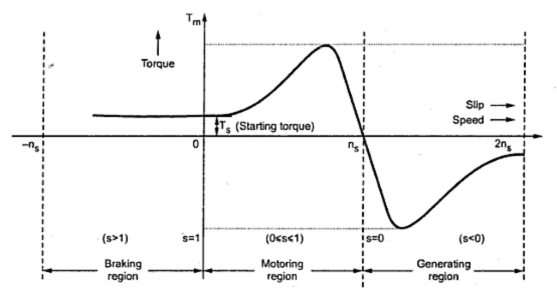
Figure: Torque-Slip Characteristics

The torque is zero While slip is zero; (N_r = N_s). We have already discussed that induction motor torque is zero at synchronous speed. At slip S_m, T; the motor gives the maximum torque that is also called as break down torque. While the rotor is stand still (S = 1), the torque corresponds to beginning torque T_s. In normally designed motor T_s is much less than T_max (Break down torque). The torque slip characteristics from no-load to rather beyond full-load are almost linear.

The condition for maximum torque

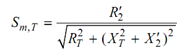
where S_{M, T} is the value of slip at which maximum torque occurs, and the maximum torque is then

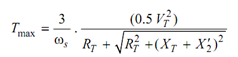
From the Eq. (59), we came to the conclusion that the maximum value of the torque does not based upon rotor resistance ( R₂′ ) .

The slip at which maximum torque occurs indirectly proportional to the rotor resistance ( R₂′ ) . At S = 1, we have the beginning torque which increases by adding resistance in the rotor circuit.