Inductances in Terms of Reluctance:

Self Inductance

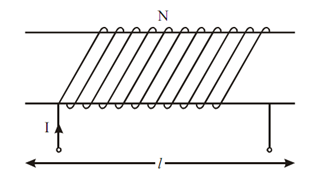
Figure: Solenoid

Figure shows the solenoid of length 'l' meter, cross-section of 'A' m², have turns 'N' over it. If this solenoid carries a current I, then magnetizing force H is specified by :

H = NI /l      AT/m

Flux linked per turn :

φ= BA = μ HA

 [? B = μ H ]

where μ = permeability. From Eq. (3)

 ψ= LI

or         L = ψ/ I = N φ/ I

Put value of φ from Eq. (17)

L = (N (μ HA) )/ I

Put value of H from Eq. (16)

L = N μ N IA / lI

= N ² μA/ l

= N ² / (  l  / μA)

= N ²/ S

where S = reluctance of magnetic circuit in AT/wb

=   (  l  / μA)

In practice, self inductance of short solenoid in given by

L = K (N ² /S)

where K = Nagoka's constant which based on the ratio of length to diameter of solenoid.

By analogy, formula for M is,

M = N₁ N₂  / S Henry

where  N₁ = no. of turns of coil 1

N₂ = no. of turns of coil 2

 S = reluctance = l / μ₀ μ₁ A

So, the inductance of a coil based upon the number of turns, the relative permeability of the core material, area of cross-section of the coil and length of the coil.