Quantity Volume Index Numbers

The Price index numbers measure and allow the comparison of the price of certain goods, the quantity index number on the other hand measure the physical volume of the production construction or employment though price indices volume of production construction or employment though hike indices are more widely used. The Production indices are highly significant as indicator of the level of output in the economy or in parts of it.

In constructing Quantity index numbers, the problems comes in front of the statistician are analogous to those involved in price indices. We measure the changes in the quantities and when we weight we use prices or values as weights, quantity indices can be obtained easily by changing p to q and q to p in the different formulae discussed above.

Thus when Laspeyres technique is used q₀₁₌Σ a₁ p₀/Σ q₀ p₀ x 100

When Paasche formula is used  q₀₁ = Σ q₁ p₁ / Σ q₀ p₁ x 100

When fisher formula is used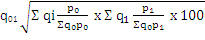   

These formulae represent the quantity index in which the quantities of the various commodities are weighted by their prices. However, any other suitable weights may be used instead.

Illustration:
                                     
From the following data compute a quantity index

Solution:
                                         
Computation of quantity index

q₀₁ = Σ q₁ p₀/Σ q₀p₀ x 100 = 2,250 / 1,900 x 100 = 118. 42

Thus as compared to 2008 the quantity index has gone up by 18.42 percent in 2009,

Illustration:
 
Compute by fisher index formula the quantity index from the data given below:

Solution: As we are given the value and the price we can obtain the quantity figure by dividing value figures by price for each commodity we can then apply fisher's ideal formula:

Computation of quantity index by fisher's method

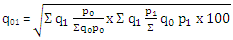
= √280/232 x 234 / 194 x 100

= √1.45574 x 100 = 1.2065 x 100 = 120.65