Perfect Multicollinearity Case:

Let us first  consider  the case of perfect multicollinearity, defining  the deviations from sample mean:  

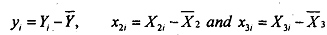
where 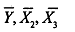are the sample means of the variables respectively. By  definition, the coefficient β₂ in MLRM is calculated as,

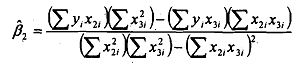
For perfect multicollinearity in our earlier example, we have assumed  X₃= 1OX₂.  Let us make it more general and assume X₃ = λx₂,  where λ is a constant as before. This implies  that in deviations form we can write  x₃  =  λ₂.Substituting  this in equition we get,

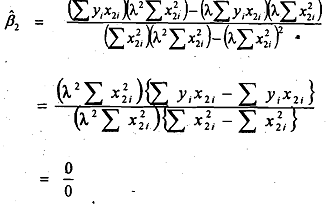
which is an  indeterminate expression. Thus the coefficient β₂  is not determinate, i.e.,  it cannot  be estimated. Similarly we can show  that the coefficient for β₃ is also indeterminate  in the presence of perfect multicollinearity.