Inefficient Provision of Public Goods:

Suppose we  have  a  public  good but  we  can exclude people  from  using  it. Remember  that it does not involve extra cost  to let someone use a public good (e-g.,  a park).  If we try to charge people to let them in and set the price higher than what  is worth  to  the least  park-liking person,  then we  end up with  an inefficient outcome. Any price that  results in the exclusion of a visitor  is too high since all people benefit from the park.  Since we cannot charge an entry fee, and  therefore, we  have  to collect  the  resources  for  it  in some way  that does not discourage  its use. We can charge different prices to different people, but  that is there is a need to devise some pricing scheme where people would correctly reveal  how much  the  park is worth  to  them.  However,  it  is very difficult  to get people to reveal what a public good is worth them.

The non-rival nature of public good consumption has important bearing on (I) what  constitutes efficient resource allocation,  i.e.,  allocation of  resources  to produce  at  least cost what  consumers want most,  and  (2)  the procedure  by which  their  provision  is  to  be  achieved. These implications  will  now be examined'more carefully when we  compare it with  the provision of private
goods as shown in the figure below.  

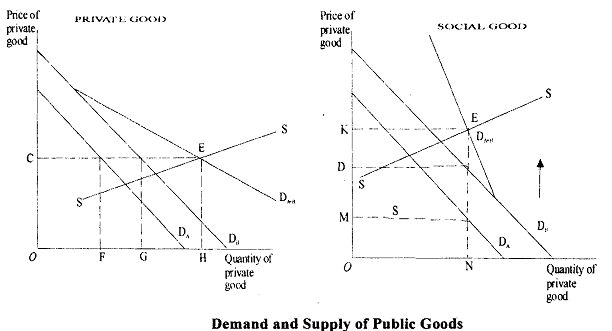
To  explore  problem 1,  it  is helpful  to compare  the  familiar demand and supply diagram for private  goods  with a corresponding construction  for public goods,  as they would  compare  in  a  hypothetical market  setting. The latter,  as we will  see presently,  is unrealistic, but  it  is nevertheless useful  in noting essential differences between the two situations. The left side of Figure 16.8 shows the conventional market for a private good. DA  and DB  are A's and B's demand curves, based  on  a given distribution of  income  and  prices  for other  goods.  The  aggregate  market  demand  curve  DA +  B  is  obtained  by horizontal  addition  of  DA and  DB, adding  the  quantities which  A and  B purchase  at  any given price.  SS  is  the supply schedule, and  equilibrium  is determined at E, the intersection of market demand and supply. Price equals OC and output OH, with  OF purchased by A  and OG by  B, where OF + OG = OH. The  right  side of  the  figure shows a  corresponding pattern  for a  public good.  We  assume  for  this  purpose that consumers  are willing  to  reveal their marginal  evaluations of  the public  good-say,  weather  forecasting installations-it  being understood that daily reports will be available free of charge.  As  before DA and  DB are A's  and B's respective demand curves, subject to the  same conditions of given incomes and prices for other goods. Since  it  is  unrealistic  to assume  that  consumers volunteer  their preferences, such curves have been referred to  as "pseudo-demand curves." But  suppose for  argument's sake that consumer preferences  are  revealed.  The  critical difference  from the private-good  case then arises in  that the market demand curve DA +  B  is  obtained  by  vertical  addition  of DA and DB, with DA + B showing the sum of the prices which A and B are willing to pay for any given amount. This follows because  both  consume  the  same  amount  and each  is assumed to offer a price  equal  to his or her  true evaluation of the marginal unit. The price available  to cover the cost of the  service equals the  sum of prices paid  by  each. SS  is again the supply schedule, showing marginal  cost (chargeable  to A and B combined)  for various outputs  of  the  public good.

The level of output corresponding  to equilibrium output OH in  the private- good case now equals ON, which is the quantity consumed by both A and B. The combined price equals OK, but  the price paid by A  is OM whereas that paid by B  is OL, where OM + OL = OK Returning  to the case of the private good, we  see that  the vertical  distance under each  individual's  demand curve reflects  the marginal  benefit, which derives  from its  consumption. At equilibrium  E,  both  the marginal  benefit derived  by  A  in  consuming OF  and  the marginal benefit derived  by  B  in consuming  OG  equals  marginal  cost  HE.  This  is  an efficient  solution
because marginal benefit  equals marginal cost for each  consumer. If output falls  short  of OH, marginal benefit  exceeds marginal  cost  and  individuals will be willing to pay more than  is needed to cover cost. Net benefits will be gained by  expanding output so  long  as  the  marginal benefit  exceeds the marginal  cost  of so  doing,  and net benefits  are  therefore maximised by
producing OH units,  at which point marginal benefit  equals marginal  cost.

Welfare  losses would occur were output expanded beyond OH, for marginal cost would thereby exceed marginal benefits. Let  us  now compare  this  solution with  that  for  public goods.  While  the vertical  distance under  each individual's demand curve again reflects the marginal benefits  obtained,  the  marginal  benefit generated  by  any given supply  is  obtained  by  vertical addition. Thus, the equilibrium point  E  now reflects the equality  between  the  sum  of the  marginal benefits  and  the marginal cost of the public good. If output falls short of ON,  it will again be advantageous to  expand because  the  sum  of  the marginal benefits exceeds cost.  An  output  in  excess of  ON,  on the  contrary, would imply welfare losses, since marginal costs outweigh  the summed marginal benefits. Thus the  two  cases are analogous but with the important difference. For  the private good, efficiency requires equality of marginal benefit derived by each individual with marginal  cost.  In  the  case  of  the  public good, on the other
hand,  the marginal benefits derived by  the two consumers differ and it is the sum  of  the marginal benefits (or marginal  rates  of  substitution) that  should equal marginal cost.

The figure also shows that an application of the same pricing rule where the price payable by each consumer equals the individual's marginal benefit yields different results for public and private goods. In the private-good case, A and B pay  the same price but purchase different amounts, whereas  in  the public good  case, they purchase  the same amount  but pay  different prices. Yet  in both cases, the same pricing rule is applied. Each consumer pays a single price for  successive units  of  the  good purchased, with  the  price equal  to  the marginal benefit that the purchaser derives.