Impedance:

No circuit is without some resistance or whether desired or not. A Resistive and reactive components in an AC circuit oppose current flow. A whole opposition to current flow in a circuit depends on its reactance, its resistance, and the phase relationships among them. Impedance is defined as the total opposition to current flow in a circuit. Equation (8-6) is the mathematical representation for the magnitude of impedance in an AC circuit.

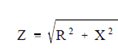
                                                 (8-6)

 where

Z  = impedance (  ? )

R  = resistance ( ?  )

X = net reactance ( ?  )

The relationship among resistance, reactance, and impedance is display in Figure.

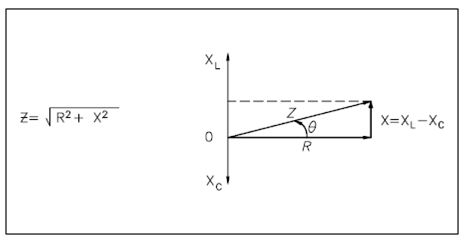
Figure: Relationship between Resistance, Reactance, and Impedance

The current by a certain resistance is always in phase along with the applied voltage.  Resistance is display on the zero axes.  The current through an inductor lags applied voltage by 90°; inductive reactance is shown along the 90° axis.  Current by a capacitor leads applied voltage by 90°; capacitive reactance is display along the -90° axis.   A Net  reactance  in  an  AC  circuit  is  the difference  among  inductive and  capacitive  reactance. Given equation (8-7) is the mathematical representation for the calculation of net reactance when X_L is greater than XC.

X = X_L - X_C                                                                 (8-7)

where

X   = net reactance (?)

X_L = inductive reactance (?)

X_C = capacitive reactance (?)

The Equation (8-8) is the mathematical representation for the calculation of net reactance when X_C is greater than XL.

X = X_C - X_L (8-8) Impedance is the vector sum of the resistance and net reactance (X) in a circuit, as display in Figure.  The angle is the phase angle and provides the phase relationship among the applied voltage and the current. The Impedance in an AC circuit corresponds to the resistance of a DC circuit. The voltage drop across an AC circuit element equals the current times the impedance. Given Equation (8-9) is the mathematical representation of the voltage drop across an AC circuit.

V = IZ                                                 (8-9)

where

V = voltage drop (V)

I = current (A)

Z = impedance (?)

The phase angle θ provides the phase relationship among current and the voltage.