Complex number vectors:

Complex numbers can be represented as the vectors in complex plane. This gives each complex number a specific magnitude and direction. The magnitude is distance of the point a +jb from origin 0+ j0. The direction is angle of the vector, which is measured counterclockwise from the a-axis. This is shown in  the Figure given to us.

Absolute value

The absolute value of the complex number a+jb is length, or magnitude, of its vector in the complex plane, measured from origin (0,0) to point (a,b).

 
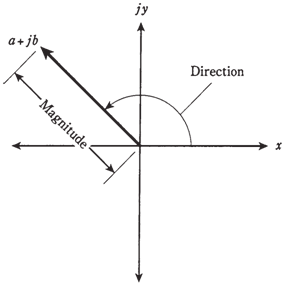
Figure--   Magnitude and direction of a vector in complex number plane.

In case of a pure real number a+j0, the absolute value is the number itself, a, if it is positive, and -a if a is negative in nature.

In case of a pure imaginary number 0+jb, the absolute value is equal to b if b (a real number) is positive, and -b if b is negative in nature.

If number is neither pure real or pure imaginary, the absolute value should be found by using the formula. First, square a and b both. Then add them. Then, take the square root. This is the length of vector a + jb. The situation is shown in the Figure given below.

 
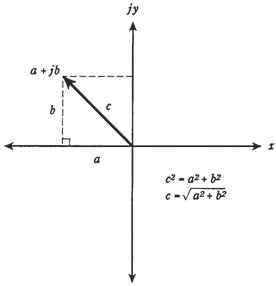
Figure--   Calculation of absolute value, or vector length.

Problem: 

Find out absolute value of the complex number -22 - j0.

Keep in mind that this is a pure real. Actually, it is same as -22+j0, as j0 = 0. Thus, the absolute value of the complex number is - (-22) = 22.