Complex number plane:

The real and imaginary numbers can be thought of as the points on a line. Complex numbers lend themselves to notion of points on the plane. This plane can be made by taking the real and imaginary number lines and placing them together, at the right angles, so that they intersect at zero points, 0 and j0. This is shown in the Figure given below. The result is a Cartesian coordinate plane, similar to the ones you use to make graphs of everyday things such as bank account balance versus time.

Notational neuroses

On this plane, the complex number can be represented as a+jb, or as a -bi, or as an ordered pair (a, b). Wait you ask. Is there a misprint here? Why b go after j, but in front of i?" The answer can be given as: Mathematicians, engineers, physicists do not think alike, and this is but one of the myriad ways in which this is apparent. Or ew can say that it is a matter of

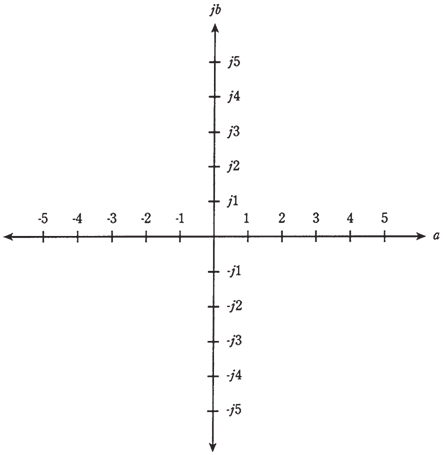
Figure--   The complex number plane.

notational convention, and this is all. (It is also a humorous illustration of the different angle which an engineer takes in approaching the problem, as opposed to the mathematician.)