Solution to Problems of Direct Central Impact:

With the additional Eq. (6), all of the five unknowns may be determined to analyse the complete problem. The difficulty referred above has direction of impact along the line joining centres of the two masses. This kind of impact is referred to as direct central impact. Solving out Eqs. (2) and (3).

m₁ (V_c - V₁) = - m₂ (V_c - V₂)

V_c (m₁ + m₂) = m₁ V₁ + m₂ V₂      

Solving Eqs. (4) and (5)

m₁ (V₁′ - V_c) = - m₂ (V₂′ - V_c)

or m₁ V₁′ + m₂  V₂′ = V_c  (m₁  + m₂ )

From Eqs. (7) and (8), we note down that

m₁ V₁ + m₂  V₂  = m₁ V₁′ + m₂  V₂′ = (m₁  + m₂ ) V_c

Which is nothing however the principle of conservation of linear momentum.

Considering ratio of Eqs  (2)/ (3)  and (4)/(5)

m₁ (V_c  - V₁ ) / m₂  (V_c  - V₂ ) = m₁ (V₁′ - V_c ) /m₂  (V₂′ - V_c ) = - 1

Also Eqs. (2) /(4) and  (3) /(5) = 1/ e  gives

V_c - V₁ / V₁′ - V_c = V_c - V₂ / V₂′ - V_c = 1/ e

∴ e (V_c  - V₁ ) = V₁′ - V_c

And e (V_c  - V₂ ) = V₂′ - V_c

Eqs. (10(a)) and (10(b)) shall eliminate unknown V_c and provide

C (V₂  - V₁ ) = V₁′ - V₂′

i.e. Coefficient of restitution

e = V₁′ - V₂′ / V₂ - V₁ = (V₂′ - V₁′) / V₁ - V₂

∴ e = Velocity of departure / Velocity of approach

If the coefficient of restitution for steel to steel is to be attained experimentally, the simplest method would be to take a spherical solid steel ball and drop it over horizontal steel plate kept on a rigid platform from a apparent height H₂ and measure the height H₂′ to which it can rise

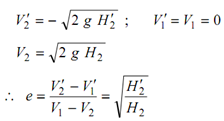
Note that final velocity of the two masses may be determined analytically, with the help of only two Eqs. (9) and (10(c)), if value of e is known.