Oblique Central Impact:

Figure illustrates two spherical masses m₁ and m₂ whose initial velocities V₁ and V₂ are not collinear. It is supposed that impulsive forces act normal to the surfaces of contact. For purpose of convenience, the common tangent at the point of contact of the two spherical masses is supposed along x axis as shown in the figure.

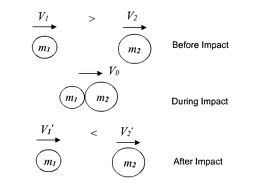
Therefore the line joining centres of the two spheres represents y axis. In such a case of

Oblique-Impact V₁, V₂, θ₁ and θ₂ are given and four unknowns are:

a.      Final velocities - (V₁′ and V₂′) , and

b.      Their directions - (θ₁′ and θ′₂ )

Let V_{1 x} , V_{2 x} , V_1x ', V_2x' be the components of velocities in the x direction. Let V_{1 y} , V_{2 y} , (V_1y )' , (V_2y)' be components of velocities in y direction. We may now consider two vector equations along x and y directions for the principle of conservation of momentum.

∴ m₁ V_{1 x +} m₂ V_{2 x =} m₁ (V_1x)' + m₂ (V_2x)'

And ∴ m₁ V_{1y +} m₂ V_{2y =} m₁ (V_1y)' + m₂ (V_{2 y})'

Figure 8.20

Since the impulsive forces may act only in y direction normal to the surface of contact, we have

∴( V_2y )' - (V_{2 y} )' = e (V_1y  - V_2y )

Since impulsive forces in x direction are not developed the component of velocities in X direction is not altered.

∴ (V_1x )' = V_1x

   (V_2x )' = V_2x