Impact of Two Bodies:
Consider a case of impact of two small spherical bodies of masses m1 and m2 moving with an initial velocity V1 and V2 along same direction say OX.
(a) Velocity of Approach = v1 - v2
(b) Contact Established t = t1
(c) Maximum-Deformation; (d) Velocity of Separation (v′2 - v1 ). At = t = t 2
Maximum-Contact Area; Masses are just separating.
(∴ Common Velocity = vc at t = t c )
Figure 8.18 : Impact of Masses m1 and m2
If v1 > v2 , then (v1 - v2 ) is relative velocity of mass m1 with respect to mass m2. This relative velocity is referred to velocity of approach. Let us say that the two bodies collide at instant t = t1 when the distance between them is specified by
[ x2 (t) - x1 (t )] = r2 + r1
where, r1 and r2 are the radii of the two spherical masses m1 and m2 , respectively. The interacting forces F between the two masses start at ( t = t1 ) while the contact is just established and magnitude of this force F because of impulse increase very fast to its maximum value F¯ at t = tc and then drop down again to zero at ( t = t2 ) when the contact is just lost. The total duration of impulse = (t2 - t1 ) .
After the impact has started at t = t1 , the velocity of mass m2 shall increase while velocity of mass m1 shall decrease till the two masses reach a common velocity Vc at time t = tc .
During this period (tc - t1 ) it is noted that there shall be deformation of both the bodies and maximum deformation as shown in Figure (c) will occur at t = tc .
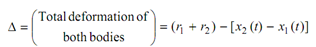
At the time of maximum value of Δ
d Δ/dt = 0 = [ d/ dt (x2(t)) - d/dt(x1(t))]=x?2(t) - x?1(t)
∴ x? 1 (t) = x? 2 (t ) = Vc at t = tc