Elastic Impact:

While the two bodies undergo fully elastic deformation under impact, they completely recover their original diameter during the period of restitution. In such collision or impact, there is no permanent deformation left in any of the body. Therefore for the elastic impact

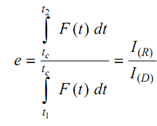
Therefore, in this case,

Velocity of departure = Velocity of approach

 (i)        Total kinetic energy of the system of two particles before impact

= m₁  (V ₁)²/2 + m₁  (V ₂)²/2    

 (ii)       Total kinetic energy of the system after impact

m₁ (V₁′)² / 2+ m₂  (V₂′)² /2

The balls are assumed to move over a smooth horizontal plate which is considered as datum level itself. Potential Energy of the balls remains constant and is assumed as zero.

The loss in KE

= m₁/2  ((V₁) ²  - V₁ ′) = m₂ /2 (V₂ )² - V ₂′)

= (½) (1 - e²) m₁ m₂ / (m₁ + m₂) (V₁- V₂)²

Under perfectly elastic impact since

                                            e = 1

Loss of KE = 0

or, Kinetic Energy is conserved.