Stresses Due to Bending Loads:

let a simply supported beam as illustrated in Figure subjected to an impact load produced by a weight W falling from a height h. This will be supposed that the weight of the beam might be neglected in comparison with W & that the work completed by W is completely transformed into strain energy of bending.

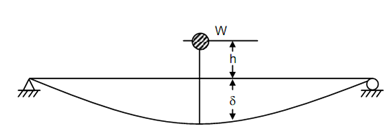
Figure

After that, the strain energy, U = Work done by W = W (h + δ)

where δ is the immediate maximum deflection under the load W.

If we is an equivalent static load which, while applied slowly, produces the same deflection as the impact load W, the work completed by We shall be equal to the work done by W.

i.e.       1/2 We δ= W (h + δ)

Let δ_st be the deflection of the beam if W were applied slowly. After that, by the linear relationship of load to deflection, it might be written

W / δ_st  = W_e / δ  or  W_e  = W × (δ /δst)

Put this in the above work equation, we achieved

(W/2) ×  (δ/ δst) × δ = W (h + δ)

 On simplifying, we have

= δ²  - 2δ_st   δ - 2δ_st  h = 0

Solution of this quadratic equation provides

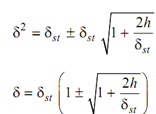
This then shall be the instantaneous deflection under the impact load W.

Once δ is known one may obtain us and the maximum bending moment, M_max produced in the beam by the application of We. After that, the maximum stress σ_max occurring in the beam might be obtained from the bending equation as

                                 σ_max  = M _max C/ I ,

here I is the moment of inertia for the cross-section & C is the extreme fibre distance from the neutral axis.