Stresses Due to Axial Loads:

Let the problem of a vertical rod of strength L & cross-sectional area A illustrated in Figure. A load W, concentric along the rod and free to slide vertically, is dropped from a height h on the end stop which might be rigid collar.

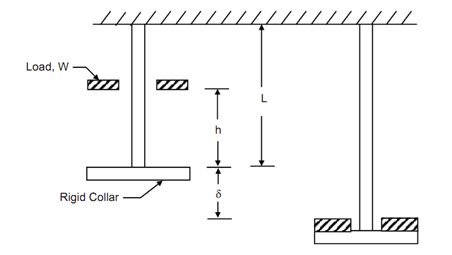
Figure

The rod is suspended from a rigid support. While the load is dropped it shall generates a maximum instantaneous extension δ in the bar, at the point of impact. After that, the load would have completed work equal to W (h + δ). Then, this ought to be equal to the strain energy stored in the bar. If σ is the instantaneous stress generated in the bar.

The strain energy, U = σ²/2E × AL

Hence, W (h + δ) =     σ² /2E AL

but

δ= σL / 2E

Therefore,

W (h + (σ L/E) = (σ2/2E) × AL

or         σ²  - (2W/ A) × σ - 2WEh/ L = 0

Denoting 2W/ A as σ_st , which would have been the stress in the bar if W were to have been applied steadily, the above equation might be written as

σ ² -   2σ σ_st  -(2Eh/L )σ_st  = 0

The solution of this equation results as follows :

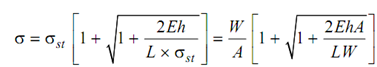
The instantaneous deflection δ then might be obtained from

                           δ= σL /E

If the load is not dropped however suddenly applied from effectively zero height (h = 0 in the above equation), the stress produced would be

                                                   σ= 2σ_st

This is a result which we have already predicted in the earlier section.

Thus, it might be seen that the stresses resulting from impact loads shall be even higher & any design work where impact loading is possible must always employ a security factor well in excess of two.