Test the Stopping Criterion

To find out the total clone size N_c generated for all of the M antigens, the given equation was employed as:

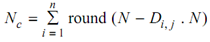
Here, N is the whole amount of antibodies in Ab, round (.) is the operator such rounds the value in parenthesis towards its closest integer and D_i,j is the distance in between the chosen antibody i and the described antigen Ag_j. In illustrated above algorithm, Steps 1.1.1 to 1.1.7 explains the clonal selection and affinity maturation processes as like proposed by de Castro and Von Zuben in their clonal selection principle's computational implementation. Steps 1.1.8 to 1.3 react as like the immune network activity. As can be observes by the Artificial immune systems based data analysis learning algorithm, a clonal immune response is elicited to all presented antigenic patterns. Observe also, the existences of two suppressive steps in this algorithm are as 1.1.9 and 1.3, such we call clonal suppression and network suppression, respectively. As far as a dissimilar clone is generated for all antigenic pattern presented, a clonal suppression is essential to eliminate intra-clonal self-recognizing antibodies, whilst network suppression is needed to search for similarities in between various sets of clones.

The network antibodies show internal images of the antigens or groups of antigens shown to it after the learning phase. The network outputs can be consider to be the matrix of memory antibodies' co-ordinates (Ab_{m}) and their matrix of affinity (S). Whilst matrix Ab_{m} shows the network internal images of the antigens shown to the artificial immune systems

Based data analysis model, matrix S is causes for determining that network antibodies such are linked to each other, explaining the general network structure. To estimate the convergence of artificial immune systems based data analysis model, some alternative criteria can be represented as:

(a)   Stop the iterative procedure after a previously explained number of iteration steps;

(b)   Stop the iterative procedure whilst the network reaches a previously explained number of antibodies;

(c)    Estimate the average error in between every antigen and the network memory antibodies (Ab_{m}) by computing the distance from all networks antibody to all antigens, this strategy will be helpful for less parsimonious solutions, and stop the iterative process if such average error is larger than a pre-specified threshold; and

(d)   The network is assumed to have converged if its average error ascends after k consecutive iterations.