Scaling:

x′ = x * S_x and y′ = y * S_y

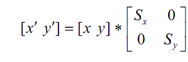
Therefore if we wanted to rotate and scale the object, the following can be done

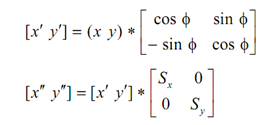
Or this may be

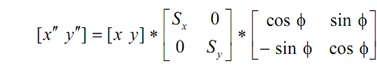
At this point, it is significant to note that we may apply number of transformations to the object at a time. But it is inefficient especially when object has several points. Thus, It is suggested to compose the transformation into one that may be applied. Therefore, we have concatenated the rotation & scaling matrices.

But the similar may not be applied in the case of Translation

                                     x′ = x + T_x

                                     y′ = y + T_y

In this case 2-D space is embedded into 3-D space. Also, all of the coordinates are expressed in the homogeneous coordinate system. If we let w = 1 so the

3-D vector becomes (x, y, 1). Then translation is represented by T = [T_x, T_y].

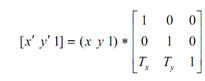
that gives

x′ = x + 1 * T_x

y′ = y + 1 * T_y