Rotation about any Point:

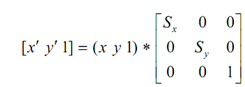
which again provides

x′ = x * S_x

y′ = y * S_y

Rotation is shown by R (q) :

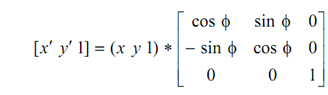
which gives

x′ = x cos φ  - y sin φ

y′ =  y cos φ + x sin φ

So this is clear that to rotate or scale an object about any point P₀ (x₀   y₀), the following have to be done

1.      Translate P0 to origin : T (- x₀, - y₀)

2.      Rotate R (q)

3.      Translate back to P0; T (+ x₀, + y₀)

So (x′ y′) = (x  y) * M, where M = T ((- x₀, - y₀) * R (q) * T(+ x₀, + y₀).

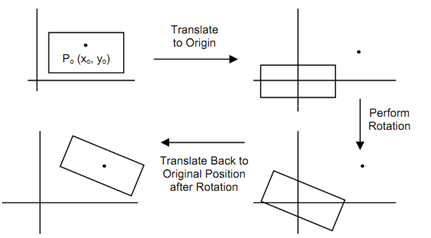
Figure: Rotation about any Point P0 (x₀, y₀)