Determine the transformation matrix:
Determine the transformation matrix to rotate an object by 90o counter clockwise around its centre. The centre of the object is at [5, 4].
Solution
Primary translate the centre of the object to its origin by utilizing transformation matrix.
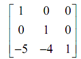
After that the rotation matrix is specified as
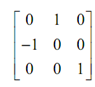
and after that translate back to the original centre by utilizing
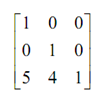
Thus the translation matrix becomes
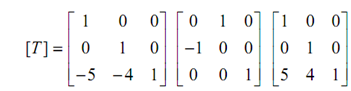
The translation matrix for rotating around any point P (p, q) through arbitrary angle may be represented as
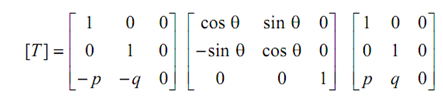
Likewise, reflection through any arbitrary axis may be accomplished by first translating an object, so that the arbitrary axis passes from the origin. After that rotating both about the origin yet the line is coincident with one of the coordinate axis. After that reflect as it has been described before and then reverse the procedure brings the arbitrary axis along with the object to its rigid position as discussed in the above example.