Torsion of Thin Tubes of Circular Section:

If the diameter of tube is large compared to its thickness (say D/t > 20), the shear stress produced because of the applied moment may be reasonably supposed to be uniform throughout the thickness. It makes the problem statically determine.

Consider external diameter D, a thin tube of length L, & thickness t, subjected to torque T as illustrated in Figure. Note t is very small compared with D. This is seen that the generator AB shall distort to AB′ while radius OB is rotated to OB′, i.e. through angle θ.

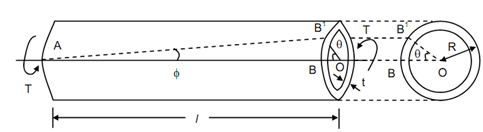
∴          Shear strain, φ= BB′ / l

Also,    BB′ = R θ

∴          φ= R θ / l

or         Shear stress, τ= G φ= GR θ / l

Free body diagram for the system is illustrated in Figure

                                                        Figure: Free Body Diagram

Letting equilibrium of forces,

T =τ × (2π R t ) × R

τ=         T / (2π R² t)

∴          τ= GR θ/ l =T/ 2π R² t

If d₀ is outer diameter, then

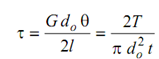
and

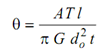
You may obtain same result by using Jh, Note down that

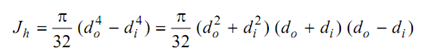
Since thickness is small, that means do - di = 2t

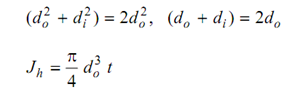
which also satisfies the definition

J_h = Area of the section × Radius square