Z-Buffer Algorithm:

Also known as the Depth-Buffer algorithm, this image-space method simply chooses for display the polygon or portion of a polygon that is nearest to the viewer, by checking the z-value of every pixel. Let us assume the quadrilateral ABCD of Figure, with the triangle EFG in front of it, and rectangle : PQRS behind it.

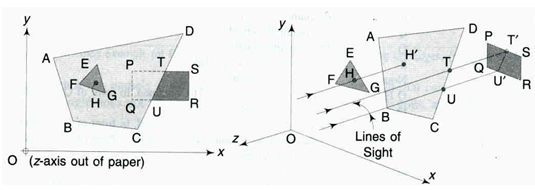
(a)                                                                  (b)

Figure: Z-Buffer Algorithm : (a) Front View; and (b) Practical View

As illustrated in Figure (a), for any point H in the triangle, its projection H′ on the quadrilateral will be behind H, and ZH shall be less than ZH′. Therefore, the entire triangle EFG shall be visible.

Alternatively the rectangle PQRS is partially hidden by the quadrilateral, the portion PQUT being hidden and the portion TURS being visible. This shall be mathematically known by the fact that for all points (x, y) within the region PQUT, the Z for the quadrilateral shall be less than the Z for the rectangle, whereas for all points within the region TURS, there shall be no common (x, y) between the quadrilateral and the rectangle, leaving just the rectangle portion to be visible.

The rays for the determination of H ′, T, and U ′ from H, T, and U are illustrated in parallel projection in Figure (b). The z-buffer memory size by this method is only dependent on the viewport, and any number of polygons may be handled.