The Rent Extraction-Efficiency Trade-Off:

The Optimal Contract Under Asymmetric Information

In the optimum, the incentive compatibility and participation constraints must bind. To solve the problem, let us first consider contracts without  shutdown, such that  q >  0  and try to eliminate the irrelevant conditions. Note that the  8-agent's  participation  constraint  is  always  strictly- satisfied.  Indeed, immediately imply seems irrelevant because the difficulty comes from a  -agent willing to claim that she is inefficient rather than efficient. When these are taken into account, we  are left with only two remaining constraints, viz.,  the  -agent's  incentive compatible constraint and the  θ-agent's  participation constraint (4.24). Both constraints must be binding  at the optimum of the principal's  problem.
Thus,  

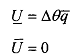
Substituting (4.25)  and (4.26)  into the principal's, objective function,  we obtain a reduced  form  of the problem  (P') with  outputs as the  only choice variables:

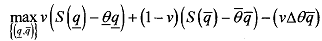
If we  recall the  solution obtained in case of full information setting, it can be seen that the asymmetric information has changed the principal's  optimisation simply by  the subtraction of the expected rent  that has to be  given up  to  the efficient type. The inefficient type gets no  rent, but the efficient type  8 gets information rent  that she could obtain by mimicking the  inefficient type θ.

Such a  rent  depends  only  on  the  level of  production  requested from  this inefficient  type.

The first order conditions are then given by

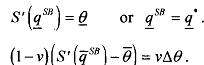
The  second of the above equations, i.e.,  (4.28) expresses the important trade- off  between  efficiency and  rent  extraction which arises  under asymmetric information.

To validate our approach  based  on  the  sole consideration of the efficient type's  incentive compatible constraint,  it is necessary to check that the omitted incentive compatible constraint of  an  inefficient agent is satisfied.  i.e.,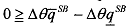This latter  inequality  follows from the second-best schedule of outputs since  we  have 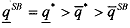with a downward output distortion  for  the  inefficient  type, 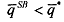with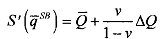

We have said above that  the complete information optimal contract (A*, B*) was  not incentive compatible. Let  us  now construct a  diagram  with an incentive compatible contract (B*, C).

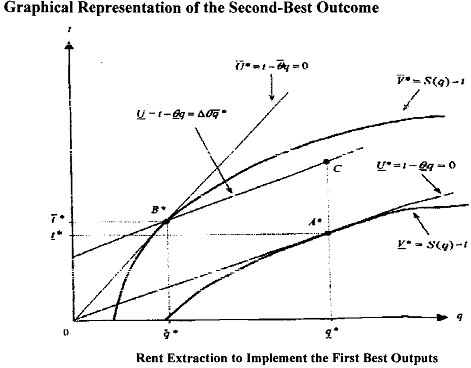
See that  it has the same production levels by  giving a higher transfer to the agent producing q* as shown in Figure. It  can be seen that the contract  C  is on  the θ -agent's  indifference curve passing through B*. Hence, the θ-agent is now indifferent between B* and C. (B*; C) becomes  an  incentive compatible menu of contracts.