The Complete Information Optimal Contract:

First-Best Production Levels

To  start with a simpler framework,  let  us first suppose that there is no asymmetry of information between the principal and the agent. By  equating the principal's marginal value and the agent's marginal cost, we get the efficient solution levels. So, first-order conditions are  

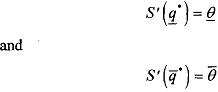
With complete information, efficient production levels  -  q* and  q'should  be both carried out if their social values, respectively 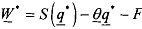  and 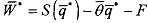are non-negative. Since

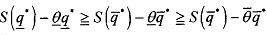
by definition of  θ and  θ > θ',  the social value of production when the agent is efficient, W*, is greater than when she is inefficient, namely, W*  . The trade is carried out as long as production is socially valuable for the least efficient type,

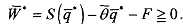
As we  enter  into  trade the fixed cost  F  does not have  any  role other than justiGing  the existence of a single agent. You can set it to zero from now. In addition, since the principal's marginal value  of  output is decreasing, the optimal production of an efficient agent is greater than  that of an inefficient agent. i.e.. q* > q'*.

.
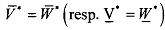