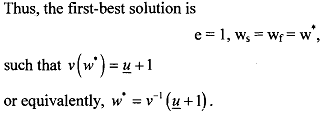Symmetric Information: First Best Option:

Start with the assumption that the principal is able to verify the agent's action. He can therefore "force"  the agent to choose e = 1. The contract that  can be offered by  the principal is (e = 1, w,,  wf) consisting of a level of effort and a wage  contingent on  the  project's outcome. The principal's expected  utility (payoff) increases with the level of effort, since  

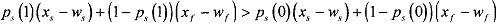
The agent will accept the contract if it yields an expected payoff  at  least as high as what she could get elsewhere, i.e.,

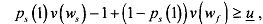
where g  denotes the agent's reservation utility. If the wages w,  and wf are not high enough. the agent will decline the offer and get g  somewhere else. The  principal's  problem  is to maximise his expected utility, subject  to the agent's participation constraint  (i.e.,  subject  to  the  agent  accepting  the contract), that is,

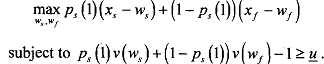
Now, we write the Lagrangian of the problem as

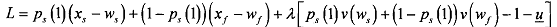
The FOC of this optimisation problem are

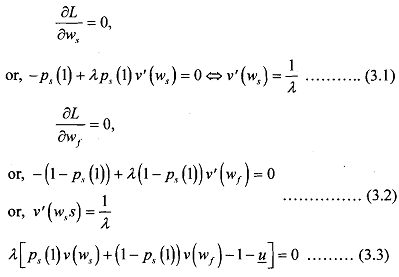
From  the  conditions and we write v'(w_f)  = 1/λ.  Since we  have  assumed v"  <  0,  this equality can only be verified if w, = w_f. When the agent is risk-averse and the principal is risk-neutral, he offers total insurance to his employee  by  offering a wage  that  is  independent from the outcome of  the project.

Thus, we get the first-best solution that a risk-averse worker if employed by a risk-neutral principal would get a wage independent of any contingency. If in the equilibrium, w_s = w_f =  w*, the agent participation constraint is

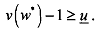
This constraint must bind. Otherwise  the  principal could lower the  wage offered w* by  a small amount, without affecting the agent's participation, but thereby increasing his own revenue.