Asymmetric Information:

If we  introduce the more realistic case where  the principal cannot verify the agent's level of effort, we get the following result:  

The principal offers a contract with a constant wage w',  the agent will decide to bunk: because she minimises her cost. The principal cannot verify this. The principal anticipates  such  a behaviour, and chooses the  wage  accordingly. What he  is trying to do is to offer a wage that maximises his expected profit, subject to e = 0.

The principal can design a contract of the form (w,, wf), such that  it pays for the agent when she actually works, i.e.,

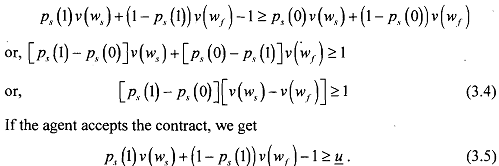
Thus, in order to get (w, - wf) increasing as (p,(l)  -  p,(O)  decreases we must have from (3.4) above w, > w,.  If there is success, the wage has to increase as its  probability decreases towards  p,(O).  It  becomes more difficult  to distinguishsomeone who works from someone who bunks. It  is  easy  to recall that condition (3.4) is incentive compatibility constraint (IC) we have seen earlier. The principal must give the agent an incentive to actually do the work. Such a design  is  compatible  with  the agent's preferences, such that when the agent maximises her  objective function, she chooses the right level of effort.

The other condition (3.5)  is participation constraint, or  individual  rationality constraint  (PC  or  IR).  It must be binding because otherwise,  it would mean that the principal would decrease both  w, and  w,  by  a small amount E  ,  which would not affect the IC constraint and would increase his expected payoff.

We can write the principal's optimisation problem as

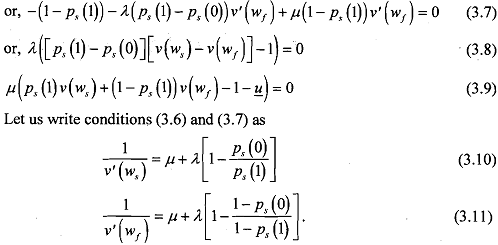
Now, we have to shown  that both constraints, IC and IR are binding. Suppose IC is not binding such that  L  = 0 ;  conditions (3.10) and (3.1 1) would  then yield 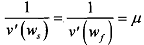and we get w_s = w_f. But  then,  v(w_s) = v(w_f) and  1C  will not  be  satisfied.  Therefore,  we  must  have λ > 0, and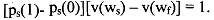 

Next, suppose IR  is not binding  such that p = 0. Condition (3.7) will not be satisfied  as  the  LHS  would always  be  negative. Therefore, you must have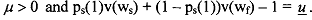

With  the constraint binding  and  p >  0,  the payment in general  to  the agent will vary with  the outcome. Thus, we  have  a situation where  the  principal desires the  action which  imposes high costs on  the agent so the payment to px  (0)

the agent will depend on the behaviour of the fraction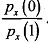

This ratio is called the likelihood ratio. It indicates the result  x  signals  that the effort was  high  (i.e., e = 1). When  the  ratio  is  smaller, p_x(l)  is higher with respect to p_x(O)  and the signal that e = 1  is stronger. Use of the likelihood ratio for the construction of the optimal incentive scheme suggests that we can use regularity conditions  found in statistics  to solve the behaviouriable problem of optimal  scheme. Let  us return to our example of employer-employee above.

We have assumed that w_s > w_f. It holds  if 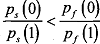 .  This implies, the ratio 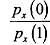decreases  when  the outcome  x  increases, just a statistical property, which we call monotonous likelihood property. Using the fact  that IC and IR bind in the equilibrium, we can have

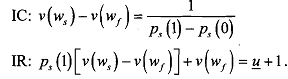
Solving for v(w,)  by  substituting 1C  and  IR,  we get  v(w_s) > v(w_f)',  (w_s) = 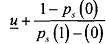. Since we  know that  the agent  is not  fblly  insured, and her -  P.7 (1) -  (0) wage will decrease in case of failure. Note  that this provides her an incentive to work.

In the above, we have tried to get the second-best situation where the principal cannot observe the action taken  by  the agent, but the outcome  only.  If  the employee (agent) receives a constant wage,  she will choose  the effort which minimises her  cost. Such an action, in general, will not be optimal. Solving the  moral  hazard problem, therefore, essentially implies that  the  employer (principal) offers the employee a contract that trade off  risk  sharing  and incentives.

The optimal incentive scheme can take  on  very  complicated forms.  The factors, which influence the optimal incentive could be profit created  by additional effort, precise assessment of desired activities agent's risk tolerance and response to incentives.