Methods of detection:

Although heteroscedasticity does  not destroy the unbiased and consistency properties of the OLS estimators, they are no  longer efficient. This lack of efficient; makes the usual hypothesis testing procedure faulty. Therefore, remedial rneasures are clearly called for. Before we make any corrections for heteroscedasticity we should first try to detect the presence of heteroscedasticity  in the error terms. Two common methods are used to detect the presence of heteroscedasticity.

1)  We plot  the  residuals 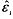 ()  against  the predicted values of the dependent variable and examine the patterns  of  residuals.  If  the variance  of  residuals  is not constant but increases  or decreases with the dependent variable, then there is a possiblityof heteroscedasticity in the data.

2)  A more careful method  is to break the sample into two or more sub-groups, each corresponding to a single value of the independent variable X, and then compute the error variance of each group. Our null hypothesis is that there is no difference among the variances of these groups. To test this hypothesis we can use  the chi-square  test assuming that  the error terms are nornlally and independently distributed. However, selection of the break point  in the data for formation of these groups is rather arbitrary. Therefore, the test is viewed to be merely an indication of the presence of heteroscedasticity.