Corrections for heteroscedasticity:

Once we have detected that there is heteroscedasticity in the error terms, we have to correct this problem. A simple method for correction of heteroscedasticity is  the method  of weighted least squares. We  discuss this estimation technique  in two conceptually separate cases based on our knowledge about the error variance. In the first case we assume that error variance  is known in  advance to us. In  the second case we assume that  the error variance increases or decreases with one of the explanatory variables.

i)  When Error Variance  is known

We assume  thatsufficient prior knowledge  is  available for values of each of  the error variances. The case of known variances occurs occasionally in econometric work but is important here in illustrating how to correct for heteroscedasticity. Recall that in the OLS method appropriate estimator is obtained by minimising  the expression

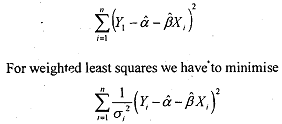
Thus each squared residual  is weighted by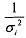. Solving for the  least-squares  parameter estimates and using the variables in deviation form, we obtain

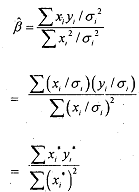
The desired estimation procedure is accomplished by weighting the original data and then performing ordinary least-squares estimation on the transformed model. Here the transformed model will be

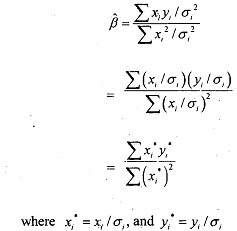
This procedure yields efficient  estimators as the transformed model by construction satisfies all  the assumptions of the classical  linear regression model. A major difficulty with this estimation method, however, is that it involves prior information on the error variances which  is not possible always. This dificulty, however, can be overcome by making certain assumptions about σ².  For example, we can estimate σ² from  the sample.