Example:

The Hermite cubic spline presents a way to describe the coefficients more meaningfully. That is, we need to define a curve by V (0) and V (1), V ′ (0) and V ′ (1), where V (0) and V (1) are the position vectors at the ends of the segment and V ′ (0) and V ′ (1) are the tangent vectors at the endpoints. The geometric significance is that the two endpoints of the Hermite cubic curve are at V (0) and V (1) and the two tangent vectors at the two endpoints are V ′ (0) and V ′ (1). It gives users a way to link two curves and assure a certain degree of continuity. An instance of particular Hermite cubic spline is illustrated in Figure. We next derive the parameter equation, given that V (0), V (1), V ′ (0) and V ′ (1) are known.

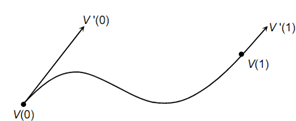
Figure: A Hermite Cubic Spline

Upon differentiation of above Equation of V (t), we have

V ′(t ) = a₁ + 2a₂ t + 3a₃ t ²

Apply boundary conditions to the above Equations

At         t = 0;    V (0) = a₀,        V ′ (0) = a₁

At         t = 1;    V (1) = a₀ + a₁ + a₂ + a₃           V ′ (1) = a₁ + 2a₂ + 3a₃

On solving these four equations simultaneously for the coefficients, we obtain

a₀ = V (0)

a₁ = V ′ (0)

a₂ = 3 [V (1) - V (0)] - 2V ′ (0) - V ′ (1)

a₃ = 2 [V (0) - V (1)] + V ′ (0) + V ′ (1)

 Put these coefficients into above equation of V (t) and rearranging gives

V (t ) = V (0) (1 - 3t ²  + 2t³ ) + V (1) (3t ²  - 2t³ ) + V ′(0) (t - 2t ²  + t³ ) + V ′(1) (- t ²  + t ³ )

V ′(t ) = V (0) (- 6t + 6t ² ) + V (1) (6t - 6t ² ) + V ′(0) (3t ²  - 4t + 1) + V ′(1) (3t ²  - 2t )

The equation may be represented in matrix form as  following:

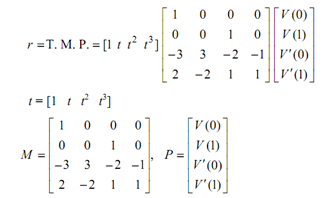
This form can be conveniently adjusted to yield several shapes of curve segment by altering one or more of V (0), V (1), V ′(0) and V ′(1) appropriately. The Hermite form of a cubic spline is found out by defining positions and tangent vectors at the data points. Hermite cubic curves are also called Ferguson's cubic curves. The equation of V (t) is a power basis representation and is good for computation.