Forces and Efficiency:

Whereas transmitting power, the force exerted through a helical gear on its mating gear behaves normal to the contracting surfaces if friction is negligible. This normal force contains three components. Given figure shows normal force 'R_n'. It may be resolved into three components namely, axial force, tangential force and radial force.

Tangential component,           ' F_t ' = R_n  cos φ_n  cos ψ

 Radial component,                  ' F_r ' = R_n  sin φ_n

 Axial component,                    ' F_a ' = R_n  cos φ_n  sin ψ                                . . . (9.12)

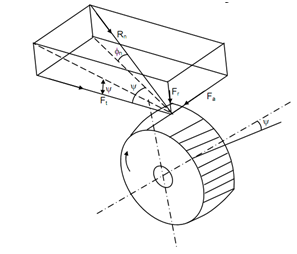
While two helical or spiral gears are in mesh the force diagrams of gear 1 & gear 2 are given in given figure. The friction force will be in horizontal plane and equal to μ F_n and shall behave opposite to the direction of velocity of sliding. Assume F is the resultant of F_n and μ F_n that is inclined with angle of friction say φ′ having F_n. Assume helix angles of gear 1 & gear 2 be ψ₁ and ψ₂, respectively. The angle among shaft axes, θ= ψ₁ + ψ₂.

Thus, for gear 1, tangential force, F_t1  = F cos (ψ₁ - φ′)  and for gear 2, tangential force,

F _t2 = F cos (ψ + φ′).

Assume tangential velocities for gear 1 and gear 2 is respectively V₁ and V₂.

Input power = F_t1 × V₁

Output power = F_t2   × V₂

 Efficiency, η

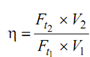
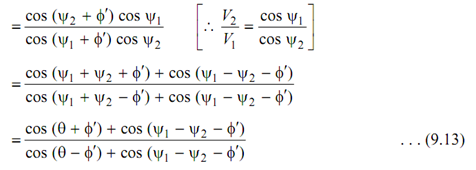
The efficiency shall be maximum if,

cos (ψ₁ - ψ₂ - φ′) = 1   or  ψ₁ - ψ₂ - φ′ = 0

 or, ψ₁ = ψ₂ + φ′  or ψ = θ+ φ′ 

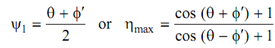                     . . . (9.14)