Sweep Representations:

The simplest form of sweep is that generated by sweeping a two-dimensional area along with an axis perpendicular to its plane. This form of sweep is most useful in representing objects that are extruded along with constant cross section or for objects that are machined to a given profile.

Another common form of sweep is to rotate a two-dimensional profile about an axis. In making a planar faceted model the profile shall be defined at a finite number of points and shall be rotated in finite steps to generate points on the surface therefore defining a polygon mesh.

It is illustrated below where the highlighted profile illustrated in Figure (a) has been rotated around the vertical axis to generate the mesh of points on the model of a wineglass illustrated in Figure (b).

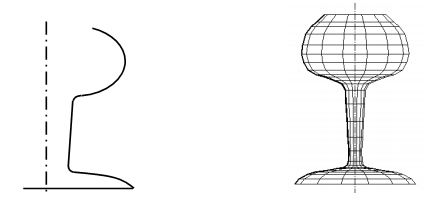
(a)                                                                 (b)

Figure: (a) 2D Profile before Sweep; and (b) Solid Formed by Sweep Rotation

Another form of sweep representation sweeps a closed two-dimensional profile along with a curve.

More complex objects may be generated by varying the size of the swept profile as it is swept along the curve, for example. a seashell could be modelled through sweeping a steadily enhancing diameter circle along a spiral curve. Though there may be difficulties caused by surfaces self-intersecting while these more advanced techniques are utilized.