H-O model:
According to the H-0 model, trade takes place in a gainful manner with important effects upon prices, wages and rents (factor prices), when countries differ in their relative factor endowments and when different industries use factors in different proportions. This is explained by Figure If two goods, X and Y, are produced with different production functions, a possible equilibrium situation is as shown in Figure. At points R and S the factors of production are allocated so that the quantities specified by the isoquants (X1 of X and Y1 of Y) are being produced at the lowestpossib/e cost given the factor prices. In other words, at R and S the two isoquants are tangential to the lowest possible isocost line, which has a slope equal to the factor price ratio, the line AB. It follows that the ratio of the marginal product of labour to the marginal product of capital is the same for the two products, and that both are equal to the ratio of the wage rate to the return to capital (the negative of the slope of the line AB).
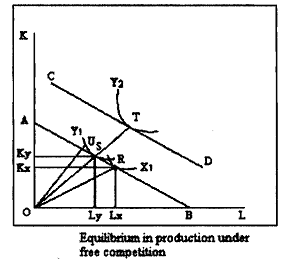
Another possible equilibrium is shown by points R and T, where again the slope of the Xisoquant at R is equal to the slope of the Y isoquant at T and both are equal to the given factor ratio. An alternative way of deriving this important result is to draw upon another standard result from microeconomics, that a producer facing given factor and producer prices will maximise his profits by purchasing factors to the point where the value of the marginal product of each factor (the marginal product times the price of the good) is equal to the price of the factor. Algebraically, using MPL and MPK to show the marginal products of labour and capital respectively, P for prices, w as the wage rate, and r as the return to capital, we have MPLyPy = w and MPKyPy = r from which it is easy to show that in order to maximise profits the producer must combine capital and labour so that
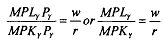
If the producer were producing good Y at a point such as Urather than point S then he would not be maximising profits. At U the marginal product of capital in producing Y is lower than it is at point S, and so the value of the marginal product of capital in producing Y at point U (the marginal product times the price of Y) is lower than the cost of the unit of capital. Similarly, the value of the marginal product of labour at point U is higher than the cost of the labour. Profits would be increased by employing more labour and less capital, the capital-labour ratio would decrease, and we would move to a point such as S or T
If for some reason factor prices were to change, factor intensities would also change. Let us assume that the price of labour compared with the price of capital increases. Then more capital-intensive methods of production will be used in both lines of
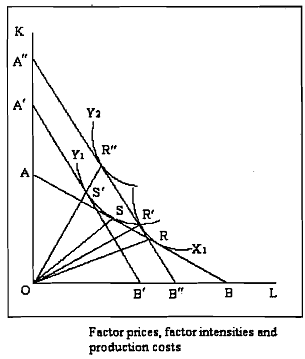
production, as shown in Figure . Before the price change OA of capital cost the same to purchase as OB of labour, but after the change OA 'of capital costs the same as OB ' of labour, and OA " of capital costs the same as OB " labour. The two budget lines A'B' and A" B" are parallel, and steeper than the original budget line AB. As labour is now more expensive and capital is cheaper than before, so that methods of production become more capital-intensive for both goods. If the desired production of X is still X, then the capital and labour combination will be at point R : and the higher capital- labour ratio in X is shown by the slope of line OR ' being steeper than that of line OR. Similarly, quantity Y, of good Y will now be produced at point S' and the slope of the line OS', and the slope of the line 0s' is steeper than that of line 0s.