Pole and Relative Pole of a Four Bar Linkage:
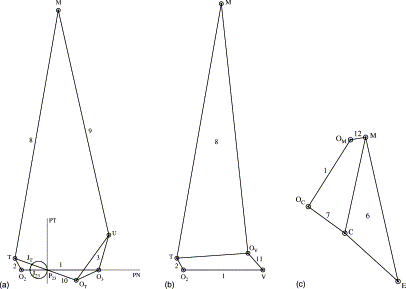
Assume a finite movement of the coupler AB of the four bar linkage from position A1 B1 to A2 B2 as illustrated in Figure. The perpendiculars may be drawn at mid points of segments A1 A2 and B1 B2. These two perpendiculars meet at P12. This P12 point is the centre for finite rotation from A1 B1 to A2 B2 and it is called the 'pole'.
Properties of Pole
(a) As AB = A1 B1 = A2 B2, the perpendicular bisectors of A1 A2 and B1 B2 pass through fixed centres O2 & O4.
(b) As coupler AB rotates around P12 from position A1 B1 to A2 B2 and, thus Δ A1 P12 B1 ≡ A2 P12 B2
∴ < 2 + < 3 + < 1 = < 1 + < 4 + < 5
Thus, Angle subtended by A1 B1 at P12 = Angle subtended by A2 B2 at P12.
(c) As < 2 + < 3 + < 1 = < 1 + < 4 + < 5
Or, < 2 + < 3 = < 4 + < 5
It means A1 A2 and B1 B2 subtend equivalent angles at P12.
(d) As P12 lies on perpendicular bisectors of A1 A2 & B1 B2
∴ < 2 + < 3 & < 4 + < 5
(e) AS < 2 + < 3 = < 4 + < 5
But < 2 = < 3 & < 4 = < 5
∴ < 2 = < 4 & < 3 = < 5
Thus, input & output links subtend equivalent angles at pole P12 as they move from one position to another.
(f) As < 2 + < 3 + < 1 = < 1 + < 4 + < 5 = < 1 + < 4 + < 3
Thus, angle subtended by the coupler is equivalent to the angle subtended by fixed link.
(g) The triangle A1 P12 B1 moves as one link around P12 to the position A2 P12 B2
Angular displacement of coupler A1 B1 = Angular displacement of P12 B1
That is < β12 = < 4 + < 5
The pole of a moving link is the centre of its rotation associated to a fixed link. But, if the rotation of the link is considered associated to another moving link, the pole is called as relative pole. To find out relative pole, fix the link of reference & observe motion of the other link in the reverse direction.