Determine the Initial compression in the spring:
In a Hartnell governor the radius of rotation is equal to 7 cm while speed is 500 rpm. At this speed, sleeve is at mid location and ball arm is normal. The sleeve movement is 2 cm along ± 5% of modification in speed. The mass of sleeve is 6 kg and friction is corresponding to 25 N at the sleeve. The mass of the ball is equal to 2 kg. If ball arm and sleeve arms are equivalent, determine the following,
(1) Spring rate,
(2) Initial compression in the spring, and
(c) Governor effort and power for 1% modification in the speed if there is no friction.
Solution
Sleeve mass 'M' = 6 kg
Friction force 'f' = 25 N
Ball mass 'm' = 2 kg
? a = b
Minimum radius r1 = 7 cm - 1 = 6 cm
Maximum radius r2 = 7 cm + 1 = 8 cm
ω= (2π× 500 )/60 = 52.36 r/s
Maximum speed = 10.05 ω = 1.05 × 52.36 = 54.98 r/s
Minimum speed = 0.95 ω = 0.95 × 52.36 = 49.74 r/s
By neglecting the influence of obliquity of arms.
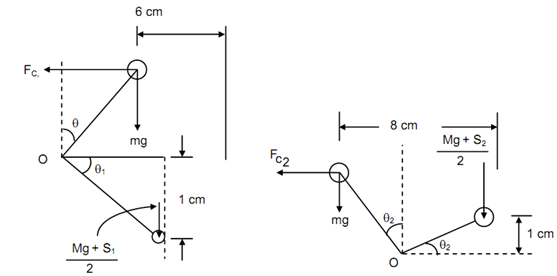
(a) (b)
At Minimum Radius
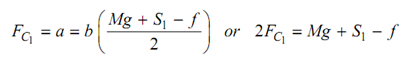
Or 2 × (49.74)2 × 0.06 × 2 = 6 g + S1 - 25
593.78 = 58.86 + S1 - 25
Or S1 = 559.92 N
At Maximum Radius
2FC2 = Mg + S2 + f
Or 2 × (54.98)2 × 0.08 × 2 = 6 g + S2 + 25
Or S2 = 883.44 N
∴ Stiffness 's' = S2 - S1 / x
= 883.44 - 559.92/ 0.02
Or S = 16175.81 N/m
Initial compression = S1 = 559.92 / 16175.81 = 0.035 m or 3.5 cm
Governor Effort and Power
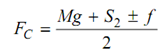
Increased speed = 1.01 ω = 1.01 × 52.36 = 52.88 r/s
At r = 0.07; 2 × 2 × (52.36)2 × 0.07 = 6 g + S
At increased speed, 2 × 2 × (52.88)2 × 0.07 = 6 g + 2 P + S
Here P is governor effort.
∴ 2P = 2 × 2 × 0.07 {(52.88)2 - (52.36)2}
Or P = 7.66 N
Assume the spring force equivalent to speed 52.88 r/s be S′.
∴ 2 × 2 × (52.88)2 × 0.07 = 6 g + S ′
∴ (S ′ - S ) = 2 × 2 × 0.07 × {(52.88)2 - (52.36)2 }
= 15.32 N
Sleeve lift for 1% change = 15.32/ s
= 15.32/ 16175.81 = 9.47 × 10- 4 m
∴ Governor power = 7.66 × 9.47 × 10- 4
= 7.25 × 10- 3 Nm