Determine equilibrium speeds:

In a Proel governor the mass of each of ball and load are equal to 5 kg and 60 kg, respectively. The length of each upper arms and lower arms are 240 mm. The upper arms are associated at the axis of the spindle and lower arms are associated at a distance of 30 mm from the axis of spindle. The lengths of links to which balls are associated are 80 mm long and they are parallel to the axis while radius is 130 mm. Determine equilibrium speeds at radii 130 mm and 190 mm.

Solution

w = 5 g N         and      W = 60 g N  (Refer to given Figure)

AB = BD = 240 mm;    BC = B₁ C₁ = 80 mm

W = 60 g,         w = 5 g

sin α= 130 /240= 0.541  or    α= 32.75^o

sin β =130 - 30/240  = 0.416   or β= 24.62^o

tan β= 0.4582 = 100/ AB′        ∴    AB′=100/0.4582== 218.25

∴          tan θ=  100/ (218.25 + 80)        or   θ= 18.54^o

∴          γ = β - θ = 24.62 - 18.54 = 6.084^o

For Radius 'r' = 130 mm

From Equation (12.6),

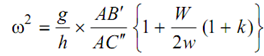
k = tan β / tan α = 0.712

AC ′'= AB′ + BC = 218.25 + 80 = 298.25 mm

h = 240 cos 32.75o  = 201.85 mm = 0.20185 m

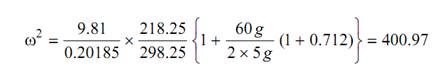
         ω     = 20.02         N₁= 191.22 rpm

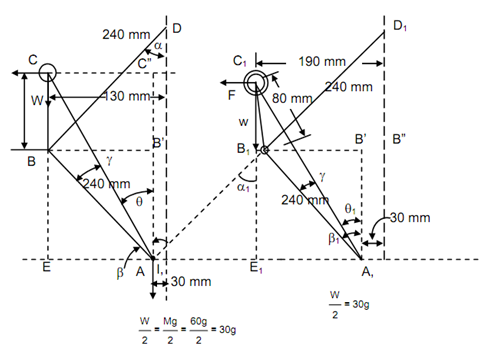
(a)                                      (b)

For Radius 'r' = 190 mm

 AC = A₁ C₁ = CC′′/sin θ = 100 /sin 18.54  = 314.5 m

sin θ ₁= 190 - 30/314.5 =  160 /314.5= 0.51

∴          θ₁ = 30.58^o

∴          β₁ = θ₁ + γ = 30.58 + 6.084 = 36.664^o

B1 B1′ = 240 sin 36.664^o = 143.31 mm

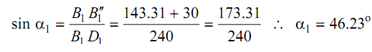
Taking moment around I₁

F × C₁ E₁ - w I₁ E₁ - (W/2) I₁ A₁  = 0

or        

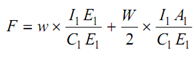
C₁ E₁  = A₁ C₁ × cos θ₁ = 314.5 cos 30.58^o = 270.76 mm

A₁′ D₁  = 240 cos β₁ + 240 cos α₁

          = 240 (cos 36.664 + cos 46.23) = 358.54 mm

∴          I₁ A₁′ = D₁ A₁′ tan α₁  = 358.54 tan 46.23 = 374.27 mm

∴          I₁ E₁  = I₁ A₁′ - A₁′ E₁  = 374.27 - 190 = 184.27 mm

I₁ A₁  = I₁ A₁′ - 30 = 374.27 - 30 = 344.27 mm

∴          F = m ω² r = 5 ω² × 0.19 N

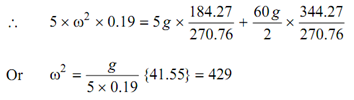
Or        ω = 20.7          or         N₂ = 197.8 rpm