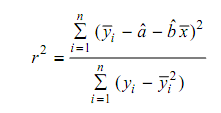Weibull Plots

 From Weibull Cumulative Density Function (CDF).

We have

 F (t) = 1 - exp [- (t/ α ) ^β] and R (t) = exp [- (t/ α) ^β]         

So,

 ln [1/{1-F(t)}] =(t/ α) ^β                              

 Taking Logarithm again,

In ln [1/ {1-F (t)}] = β ln t - β ln α    

The above Eq. (49) is of the form y = mx + c where ordinate is ln ln[1/{1-F(t)}] and abscissa is ln (t_i). Thus a plot between ln (t_i) and ln ln [1/ {1-F (t)}] is representative to Weibull probability paper plot of [t_i, F (t_i)].

Generally, a least-squares fit to the data is recommended over a manual plot of the data on probability paper. It is more accurate and less subjective than fitting a straight line to the data by eye. In addition, measures of how well the curve fits the data, such as the index of fit, are available. With the use of the personal computer and one of the many statistical applications available (MS Excel) with graphics capability, plotting data by hand is no longer necessary. Weibull graph paper is constructed so that data generated from a Weibull distribution will graph as a straight line. The abscissa is a logarithmic scale, and the ordinate, while labeled in terms of the cumulative percentage of failures, F (t), is scaled on the basis of ln ln[1/{1-F(t)}] , which can be easily calculated using the Microsoft Excel.

Alpha (α) can be estimated from the point on the line that corresponds to 63.2 percent of the failures, Since F (α) = 0.632. The 63.2 percent line is often identified on the graph paper. It can be seen from previous equation that β can be estimated from the slope of the plotted line. Once β is calculated, the value of α can be estimated using the intercept of the fitted Straight line.

 The index of fit (r) can be calculated from the following equation.