Mann's Test for Weibull Distribution

A specific test for the Weibull (2-parameter) failure distribution is a test developed by Mann, Schafer and Singapurwalla [1974]. The hypotheses are following

H₀ : The failure times are Weibull.

H₁ : The failure times are not Weibull. The test statistic is

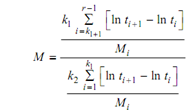
Where

k₁= [r/2]

k₂= [(r-1)/2]

M _i = z_{i +1 -} z_i         

Z_i = ln[- ln(1-i-0.5/ n+2.5)]

and [x] is the integer portion of the number x, is an approximation. If M < H, H0 is accepted and M > F then H₁, is accepted. Values for F may be obtained from tables of the F-distribution, 2 k₂ degrees of freedom for the numerator and 2 k₁ degrees of freedom for the denominator. This test is for the two-parameter Weibull distribution. So if the alternative hypothesis is accepted, the three-parameter Weibull as well as other distribution should be considered. The data must be rank-ordered for the test statistic to be computed.