Kolmogorov-Smirnov (K-S) Test for Normal and Lognormal Distributions

A goodness-of-fit test for use with the normal distribution when the parameters are estimated is a version of the Kolmogorov-Smirnov test developed by H. W. Lilliefors [1967]. It compares the empirical cumulative distribution function with the normal cumulative distribution function. The hypotheses are:

H₀: The failure times are normal.

H₁:  The failure times are not normal.

The test statistic is D_n = max {D₁, D₂} where

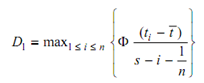
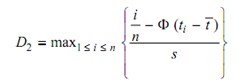
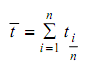
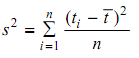
if D_n < D_crit , then accept H₀; if D_n  ≥ D_crit , then accept H₁. The values for D_crit may be found in Statistical tables. This test is appropriate for complete samples only.