Importance of Weibull Distribution

Alpha (α) is called Scale parameter of Weibull Distribution that influences both the mean and the spread or dispersion of the distribution. The effect of α can be straight away translated in terms of reliability. As α increase, the reliability increases at given point in time.

Each of the CDF and Reliability curves passes through the same point where t = α, irrespective of the value of β, since form Eq. (47), we have R (t) = exp [- (t/ α)]   and at t = α, we get R (t) = exp [- (α/ β)] = exp (- 1) = 0.368. Therefore, 63.2 percent of all Weibull failures will occur by time t = α regardless of the value of Shape parameter. Hence this parameter is also called the Characteristic Life and has the units identical to those of failure time, T.

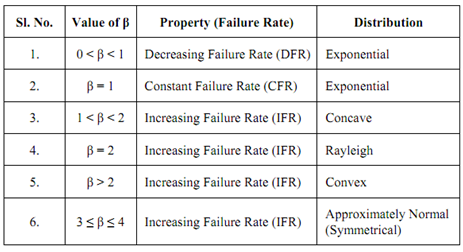
Beta (β) is referred to as shape parameter of Weibull Distribution. For β < 1, the PDF is similar to the Exponential and for large values of β (e.g. β ≥ 3), the PDF is somewhat symmetrical, like Normal Distribution. For 1 < β < 3, the Density function is Skewed.

When β =1, λ (t) is constant and the distribution is identical to Exponential with λ = 1/ α where α is the scale parameter of Weibull Distribution. Thus the hazard rate function can be increasing or decreasing depending on the value of β. This is summarized in the following Table.

                                                          Table: Weibull Shape Parameter (β) Characteristics