Chi-Square Goodness of Fit Test

This test is applicable to both continuous and discrete distributions and may be used when the parameters of the distribution are estimated from the maximum likelihood estimators (MLEs). The test is valid for large sample sizes only. The data must be grouped into classes.

Test Statistic is

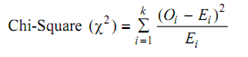
Where k = Number of classes,

O_i = Observed number of failures (or repairs) in the i^th class,

E_i = n p_i = Expected number of failures (or repairs) in the i^th class,

n = Total number at risk (sample size), and

p_i = Probability of a failure occurring in the i^th class if H₀ is true.

The probabilities are based on the distribution stated in the null hypothesis. To ensure an approximate chi-square distribution, n P_i should be at least 5 for all i or use Sturge's rule. The test statistic, χ² has a chi-square distribution with degrees of freedom equal to k - 1 - number of estimated parameters. Critical values are then obtained from Statistical Tables. On comparison, if calculated value is less than critical value, then we accept null hypothesis, otherwise we discard.