Bartlett's Test for Exponential Distribution

A specific test for fitting exponential distribution is Bartlett's test. The hypotheses are:

H₀: Failure times are exponential.

H₁: Failure times are not exponential. The test statistic is

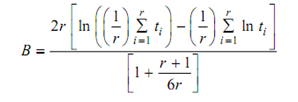
Where  t_i = time of failure of the i^th unit, and r = number of failures.

The test statistic, B under the null hypothesis, has a chi-square distribution with r - 1 degrees of freedom, in this,

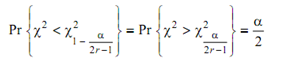
If        

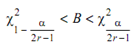
Then the null hypothesis is accepted; otherwise the alternative hypothesis accepted. Observe that the failure rate of the exponential need not be estimated to apply this test. A sample size of 20 or more failures is recommended in using this test in order to achieve an adequate power for the test to reject the exponential when appropriate. However, if Chi-Square test rejects, the Bartlett's test need not be performed.