Bezier Curves:

Bezier curves are utilized in CAD and are named after a mathematician working in the automotive industry. These are based on approximation techniques that generate curves that do not pass through all of the given data points except the first & the last control point. A Bezier curve does not needs first-order derivative; the shape of the curve is controlled by control points.

For n + 1 control points, the Bezier curve is described by a polynomial of degree n as follows :

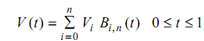        ------------ (1)

where V (t) is the position vector of a point on the curve segment and B_i, n are the Bernstein polynomials, that serve as the blending or basis function for the Bezier curve.

The Bernstein polynomial is described as

B_{i, n}  (t ) = C (n, i) t ⁱ  (1 - t )^{n - i}  =         (n!/ ( i! (n - i)! ) ) tⁱ  (1 - t )^{n - i}         --------- (2)

 where C (n, i) is the binomial coefficient specified by

C (n, i) = n! / ( i!  (n - i)!)                              ----------- (3)

Substituting Eq. (2) in Eq. (1)

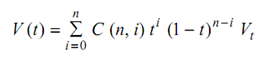
Here V₀, V₁, . . . , V_n are the position vectors of n + 1 points that form the so-called characteristic polygon of the curve segment.

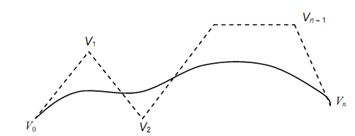
Figure: Bezier Curve and its Characteristic Polygon