Epicycloid:

If a circle of diameter D rolls on the outside of another circle of radius R, the path of the point A is like on the rolling circle is called an epicycloids as display in diagram.

To sketch the epicycloids, describe a rolling circle of diameter D and a guiding circle of radius R tangent to it at point 12. Divide the rolling circle into 12 equal parts. With O_o like a center and a radius equal to R + D/2 sketch an auxiliary arc. From the point A and clockwise layout on the guiding circle mark 12 divisions, each one equal to 1/12 π D. To find out the arc of the guiding circle AA₁₂ = π D, use the formula α =180^o D/R.

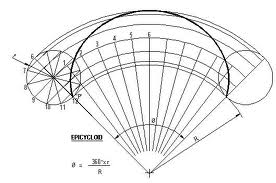
The angle α hence obtained is divided into 12 equal parts along with the aid of a protractor and the points are denoted as 1′ via 12′. From Oo and via these points draw radial lines whose extensions will intersect the auxiliary arc at point O₁ via O₁₂. Along with O_o like a center describe a series of auxiliary arcs passing via the points of division of the rolling circle.

From O₁ via O₁₂ as centers and along with a radius equal to D/2 describe arcs to intersect the corresponding auxiliary arcs at points A₁ via A₁₂. A smooth curve is then drawn via these points to get the required epicycloids.