Generalized Stochastic Petri Nets or GSPN

Generalized Stochastic Petri nets are the performance analysis tool based on the graphical system presentation typical of the Petri nets, whether few transitions are timed where as others is immediate.

The fundamental motivation behind proposing Generalized Stochastic Petri Nets is to ignore associating time to those transitions such are believed to have least impact on the performance of the system. Through the timed transitions, random exponentially distributed timed delays are connected whereas the immediate transition fire now and have a higher priority over timed transitions.

The selection between possibly conflicting enabled immediate transitions is made via firing probabilities forming the so named as random switches. Hence, mathematically we have a Generalized Stochastic Petri Nets as an eight-tuple,

(P, T, IN, OUT, INH, M₀, F, S)

Here,   (P, T, IN, OUT)

Represent the general Petri net notation and INH shows the inhibitor marked Petri net. The set of transitions is additionally partitioned into two sets:

(a)   Timed transitions or termed as also exponential transitions TE, and

(b)   Immediate transitions TI.

There exists several firing function also (F (M, t)) linked with all exponential transition T_E. For illustration consider a set of enabled exponential transitions Te in several immediate marking M_e. After that the transition t_j ∈ T_e fires along with probability,

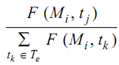
A Generalized Stochastic Petri Nets marking where merely exponential transitions are enabled are termed as tangible markings and else are known as vanishing markings.