Stability and Uniqueness:
Stability of the Walrasian equilibrium can be evaluated by specifying that the prices will adjust according to the conditions of excess demand. If at some price, demand > supply, price would rise. Conversely, if demand < supply, price would fall. Thus, if we consider change in price over time and write the excess demand equation as
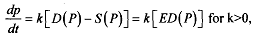
price adjustment can be seen through a solution of the equation. Recall Taylor series given in MEC-003, and write the above equation as
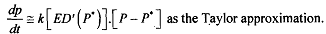
You get a first-order differential equation. The general solution to it will be
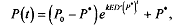
where Po = initial price at time, t = 0. Stability of the above system is ensured as
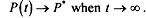
For this to happen,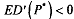
. In other words, an increase in price must reduce excess demand and a fall in price must increase excess demand.
We have seen that under certain conditions at least one Walrasian equilibrium exists. However, there could be a large number of equilibria, if equilibrium prices (P,') are unstable. Such a possibility raises the question of uniqueness of Walrasian equilibrium. Without existence of a single equilibrium, it becomes difficult to predict the movement of an economy from a set of initial conditions when we change some of the parameters. For Walrsian equilibrium is to be unique, we need to incorporate additional assumptions. One assumption that can be made it that all goods are gross substitutes at all prices.