Description of the Economy:

Let  us  consider  a  pure  exchange model  where  no  production  takes  place. Consumers have  initial bundles of goods,  initial endowments. They exchange with  each other these goods according to their preferences. For  example, you have quantities of apples and 1 have oranges. We enter into an exchange, your apple and my oranges. Note that the exchange to take, you must be willing to consume my oranges and I am willing to consume your apples.

We can think of n consumers and k commodities in the economy.  Each consumer has initial endowments and preferences. Whereas endowment refers to  the commodity held  by  a consumer, her  preferences are represented  by a utility function  y = u, 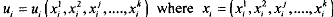 is  the i^th  individual's consumption bundle.

We  introduce a price system P such  that P = (P_I,  P_z,  ...., P_k). Note  that the economy you  are presented with, does  required  payment terms of money  as people trade one good  for another (exchange in  barter  system). But  the price we  intend  to use  is for the exchange rates. For  example, the price of one unit of good X  is one unit  good Y.  Such a price, therefore, can  be  called relative price of good X.  If  the price of Potato is Rs. 5 per kg and the price of apple is Rs. 2.5 per kg, then the relative price of Potato in terms of apple is 2 (i.e., each unit of Potato is worth 2 units of apple). Similarly,  the relative price of apples in  terms of Potato is 0.5  (i.e., one unit of apple is worth half unit of Potato).

Remember  that we will use  relative price  in  the following analysis. Imagine that the consumer  i  purchases  x,'  units of good j  at price PJ. Then PJ.X,  gives the  amount  of expenditure  incurred  by  her  and  to  that  extent  her income stands reduced. On the other hand, when she delivers goods of equal quantity, the income  t',x,'  is added to her income.

To arrive at the equilibrium of the model, let us  start with  consumer's  utility maximisation. See that the ith consumer maximises
Ui(Xi)  subject to her budget constraint PXi = PWi. Remember that solution to this  problem  yields  the  demand  functions X_i  = X,(P,  PW_i),  i  =1,2,..  .n  and demand for each commodity depends on all prices and the  initial endowment.