Competitive equilibrium:

In  selecting an economy with pure exchange, we ignore the production at this point of our analysis. Such a framework helps us concentrate on allocation of goods  that are alrea4 produced. Our concern  now is  to  find  a criterion of allocation agreed to be  'good'  enough by  the society. The framework of social welfare in which we looked for Pareto efficiency in Block 5 is invoked to see that competitive  equilibrium ensures  that.

Edgeworth Box:

As we  have  already seen a useful graphical tool for describing the feasible allocations for  the economy with  2  agents  (A, B)  and  2 goods (F,  S) is the Edgeworth box.  

The Edgeworth box  combines the x-y  axes of  the  two consumers such  that when we allocate more to consumer A, there is less available for consumer B. Figure shows the Edgeworth box  for this economy. All  the  allocations inside the box are feasible. However, the preferences do not depend on the set of feasible allocation.

Let us start with position E in  the figure, which depicts  the positions of A and B, with their initial endowments. If trade is allowed where will they end up? It is not clear because either or bath could be made better without making either worse off. However, we can  say  that they need  to be  somewhere in the lens shaped region between u_A and u_B.  Why?  Because  all these points Pareto dominate E, where Paretodominate implies the following:

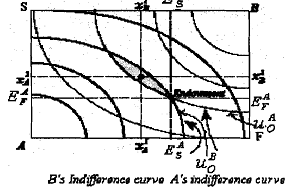
Consider  two allocations x  and  x'  . The  allocation  x'  is said  to Pareto dominate x if everyone prefers  x'  to x. In the figure one or both  parties could be  made better  off  without making the other worse  off. Thus, there  are potential gains from the trade.

Next, we look at the indifference curves of both consumers. We have assumed that the preferences are convex and increasing in  both goods. Note that it  is possible to make both  consumers better off by moving them  to allocation inside the  lens area  formed by  the indifference curves. That is,  if agents  consume their initial endowments, then this  allocation will  not  be efficient. On  the other hand,  if  there  is a possibility to make both  consumers better off, there is no reason for not doing that. In  the  figure, equilibrium  is determined at  the point where  the two  IC's  are tangent. Given the prices indicated by  the slope of the price line, both agents maximise  utility with  respect  to  their  budget  set. Thus, at equilibrium, the MRS of the two agents are equal:

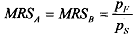
An  important result that you have to remember  is, in  the equilibrium only the relative price matters.