Brouwers fixed-point theorem:

The cumbersome process of arriving at the equilibrium price led to addition of  other methods.  Brouwer's fixed-point  theorem  is  one  of  the tools  used.  It states:
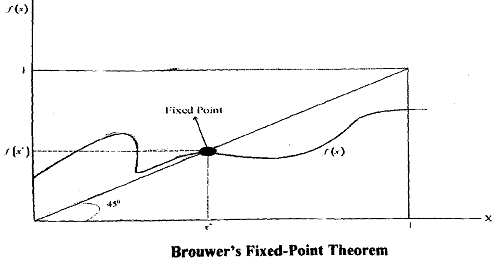
Any  continuous mapping  [F(x)] of  a closed, bounded,  convex set  into  itself  has at least one fixed point (x*)  such that                 F(x*)  = x*
To  understand  the statement, suppose  that  f(x)  is  a continuous  function defined in the interval [0, 11  and  that  it  takes on values on  the interval [0,1]. Such a function  then  obeys  the conditions of Brouwer's  theorem that  there exists some x* such that f(x*)  =  x*.  Look at Figure to understand the idea.

It  can  be  seen  from  the figure that any  function, which  is continuous, has to cross the 45'  line somewhere. The point  of crossing is a  fixed  point,  since f maps this point (x*)  into itself

The fixed-point theorem  of  Brouwer  is developed by  considering mapping  defined on certain types of sets. These set are required to be closed, bounded  and  convex. While  applying  the  theorem  to  the  exchange model, we  have  outlined above, you have to choose a suitable way to normalizing prices. If we  consider the form of normalisation.

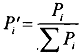
and remember  that  at  least  one of the prices  is non-zero, such transformed prices have the characteristics that

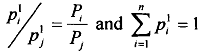Now the task is to construct a continuous function that  transforms one  set  of  prices  into another. The function  is  defined  such  that  equilibrium  is  achieved  by increasing the prices of goods that have excess demand while reducing those with excess supply.

Define mapping F(P) such that

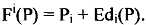
In  order to  ensure that new  prices will  be  nonnegative, the mapping of F is either  positive  or  zero. To include this condition, often  we  write,  F'(P) = Max[P_i + ED_i(P),O]. Moreover, the normalisation must satisfy the condition

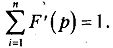
Application of Brouwer's Theorem:

With the above-mentioned normalisation process, there exists a point (P*) that mapped into itself and

The key requirement for the existence of a Walrasian equilibrium is continuity of  the  aggregate  excess  demand  function.  This is the case if consumer preferences are convex.